Solicitamos su permiso para obtener datos estadísticos de su navegación en esta web, en cumplimiento del Real Decreto-ley 13/2012. Si continúa navegando consideramos que acepta el uso de cookies. OK | Más información
Compartir en WhatsApp, sólo para móviles.

VIGAS EN VOLADIZO

RESUMEN DE CASOS

Pulsa en el diagrama para ir al caso elegido:

CASO 19

Diagrama forma y cargas caso 19

Definición

Viga en voladizo con una carga puntual intermedia.

REACCIONES

\[ \mathrm{R_B}=P \]
\[ \mathrm{M_B}=P \cdot b \]
Diagrama de cargas y reacciones caso 19

E. CORTANTES

\[ \mathrm{V_{AC}}=0 \]
\[ \mathrm{V_{CB}}=-P \]
Diagrama de Cortantes caso 19

M. FLECTORES

\[ \mathrm{M_{AC}}=0 \]
\[ \mathrm{M_{CB}}=-P \cdot (x-a) \]
\[ \mathrm{M_{máx}}=|-P \cdot b | \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 19

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{P \cdot b^2}{6 \cdot E \cdot I} \cdot (3 \cdot (L-x)-b) \]
\[ \mathrm{Y_C}=\frac{P \cdot b^3}{3 \cdot E \cdot I} \]
\[ \mathrm{Y_{CB}}=\frac{P}{6 \cdot E \cdot I} \cdot (L-x)^2 \cdot (2 \cdot b-a+x) \]

FLECHA

\[ \mathrm{Y_A}=\frac{P \cdot b^2}{6 \cdot E \cdot I} \cdot (2 \cdot b + 3 \cdot a) \]
Flecha caso 19

ÁNGULOS DE GIRO

\[ \mathrm{\theta_C}=\mathrm{\theta_A}=-\frac{P}{2 \cdot E \cdot I} \cdot b^2 \]


CASO 20

Diagrama forma y cargas caso 20

Definición

Viga en voladizo con una carga puntual en el extremo.

REACCIONES

\[ \mathrm{R_B}=P \]
\[ \mathrm{M_B}=P \cdot L \]
Diagrama de cargas y reacciones caso 20

E. CORTANTES

\[ \mathrm{V_B}=\mathrm{V_x}=-P \]
Diagrama de Cortantes caso 20

M. FLECTORES

\[ \mathrm{M_x}=-P \cdot x \]
\[ \mathrm{M_{máx}}=|-P \cdot L | \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 20

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac{P}{6 \cdot E \cdot I} \cdot (L-x)^2 \cdot (2 \cdot L+x) \]

FLECHA

\[ \mathrm{Y_A}=\frac{P \cdot L^3}{3 \cdot E \cdot I} \]
Flecha caso 20

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\frac{P \cdot L^2}{2 \cdot E \cdot I} \]


CASO 21

Diagrama forma y cargas caso 21

Definición

Viga en voladizo con una carga uniformemente repartida aislada.

REACCIONES

\[ \mathrm{R_B}=q \cdot c \]
\[ \mathrm{M_B}=q \cdot c \cdot b \]
Diagrama de cargas y reacciones caso 21

E. CORTANTES

\[ \mathrm{V_{AC}}=0 \]
\[ \mathrm{V_{CD}}=-q \cdot (x-a+\frac C2) \]
\[ \mathrm{V_{DB}}=-q \cdot c \]
Diagrama de Cortantes caso 21

M. FLECTORES

\[ \mathrm{M_{AC}}=0 \]
\[ \mathrm{M_{CD}}=-\frac q2 \cdot (x-a+\frac C2)^2 \]
\[ \mathrm{M_{DB}}=-q \cdot c \cdot (x-a) \]
\[ \mathrm{M_{máx}}=|-q \cdot c \cdot b| \hspace{2em} para \hspace{1em} x=L\]
Diagrama de momentos caso 21

EC. ELÁSTICA

\[ \mathrm{Y_{DB}}=\frac {q \cdot c}{6 \cdot E \cdot I} \cdot (L-x)^2 \cdot (2 \cdot b -a+b) \]
\[ \mathrm{Y_D}=\frac {q \cdot c}{48 \cdot E \cdot I} \cdot (4 \cdot b+c) \cdot (2 \cdot b -c)^2 \]
\[ \mathrm{Y_{CD}}=\frac {q}{24 \cdot E \cdot I} \cdot ((x-a+\frac c2)^4+4 \cdot c \cdot (a-x) \cdot (3 \cdot b^2+\frac{c^2}{4})+8 \cdot b^3 \cdot c) \]
\[ \mathrm{Y_{CD}}=\frac {q}{24 \cdot E \cdot I} \cdot ((x-a+\frac c2)^4+ ... \] \[ ... +4 \cdot c \cdot (a-x) \cdot (3 \cdot b^2+\frac{c^2}{4})+8 \cdot b^3 \cdot c) \]
\[ \mathrm{Y_{AC}}=\frac {q \cdot c}{6 \cdot E \cdot I} \cdot ((a-x) \cdot (3 \cdot b^2+\frac{c^2}{4})+2 \cdot b^3) \]
\[ \mathrm{Y_{AC}}=\frac {q \cdot c}{6 \cdot E \cdot I} \cdot ((a-x) \cdot (3 \cdot b^2+\frac{c^2}{4})+2 \cdot b^3) \]
\[ \mathrm{Y_C}=\frac {q \cdot c}{48 \cdot E \cdot I} \cdot ((4 \cdot b-c) \cdot (2 \cdot b +c)^2 + 4 \cdot c^3) \]
\[ \mathrm{Y_C}=\frac {q \cdot c}{48 \cdot E \cdot I} \cdot ((4 \cdot b-c) \cdot (2 \cdot b +c)^2 + 4 \cdot c^3) \]

FLECHA

\[ \mathrm{Y_A}=\frac {q \cdot c}{24 \cdot E \cdot I} \cdot (12 \cdot a \cdot b^2 + a \cdot c^2+8 \cdot b^3) \]
Flecha caso 21

ÁNGULOS DE GIRO

\[ \mathrm{\theta_D}=-\frac{q \cdot c}{2 \cdot E \cdot I} \cdot (b^2- \frac{c^2}{4}) \]
\[ \mathrm{\theta_C}=-\frac{q \cdot c}{2 \cdot E \cdot I} \cdot (b^2+ \frac{c^2}{12}) \]
\[ \mathrm{\theta_A}=\mathrm{\theta_C} \]


CASO 22

Diagrama forma y cargas caso 22

Definición

Viga en voladizo con una carga uniformemente repartida.

REACCIONES

\[ \mathrm{R_B}=q \cdot L \]
\[ \mathrm{M_B}=\frac {q \cdot L^2}{2} \]
Diagrama de cargas y reacciones caso 22

E. CORTANTES

\[ \mathrm{V_x}=-q \cdot x \]
Diagrama de Cortantes caso 22

M. FLECTORES

\[ \mathrm{M_x}=-q \cdot \frac {x^2}{2} \]
\[ \mathrm{M_{máx}}=|-q \cdot \frac {L^2}{2}| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 22

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {q}{24 \cdot E \cdot I} \cdot (L-x)^2 \cdot (3 \cdot L^2+2 \cdot L \cdot x+ x^2) \]
\[ \mathrm{Y_x}=\frac {q}{24 \cdot E \cdot I} \cdot (L-x)^2 \cdot (3 \cdot L^2+2 \cdot L \cdot x+ x^2) \]

FLECHA

\[ \mathrm{Y_A}= \mathrm{Y_máx}= \frac{q \cdot L^4}{8 \cdot E \cdot I} \]
Flecha caso 22

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\frac{q \cdot L^3}{6 \cdot E \cdot I} \]


CASO 23

Diagrama forma y cargas caso 23

Definición

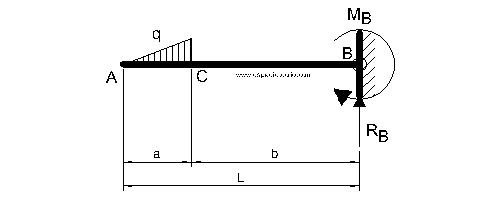
Viga en voladizo con una carga no uniformemente repartida que comienza en el empotramiento según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac{q \cdot b}{2} \]
\[ \mathrm{M_B}= \frac{q \cdot b^2}{6} \]
Diagrama de cargas y reacciones caso 23

E. CORTANTES

\[ \mathrm{V_{AC}}= 0 \]
\[ \mathrm{V_{CB}}= -\frac{q \cdot (x-a)^2}{2 \cdot b} \]
Diagrama de Cortantes caso 23

M. FLECTORES

\[ \mathrm{M_{CB}}= -\frac{q \cdot (x-a)^3}{6 \cdot b} \]
\[ \mathrm{M_{AC}}= 0 \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot b^2}{6}| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 23

EC. ELÁSTICA

\[ \mathrm{Y_{CB}}=\frac {q}{120 \cdot E \cdot I \cdot b} \cdot ((x-a)^5-5 \cdot b^4 \cdot x+5 \cdot b^4 \cdot L-b^5) \]
\[ \mathrm{Y_{CB}}=\frac {q}{120 \cdot E \cdot I \cdot b} \cdot ((x-a)^5-5 \cdot b^4 \cdot x+5 \cdot b^4 \cdot L-b^5) \]
\[ \mathrm{Y_{AC}}=\frac {q \cdot b^3}{120 \cdot E \cdot I} \cdot (-5 \cdot x+5 \cdot L-b) \]
\[ \mathrm{Y_{AC}}=\frac {q \cdot b^3}{120 \cdot E \cdot I} \cdot (-5 \cdot x+5 \cdot L-b) \]
\[ \mathrm{Y_C}=\frac {q \cdot b^4}{30 \cdot E \cdot I} \]

FLECHA

\[ \mathrm{Y_A}=\frac {q \cdot b^3 \cdot a}{24 \cdot E \cdot I}+ \frac {q \cdot b^4}{30 \cdot E \cdot I} \]
Flecha caso 23

ÁNGULOS DE GIRO

\[ \mathrm{\theta_C}=\mathrm{\theta_A}=-\frac {q \cdot b^3}{24 \cdot E \cdot I} \]


CASO 24

Diagrama forma y cargas caso 24

Definición

Viga en voladizo con una carga no uniformemente repartida que comienza en el extremo según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac{q \cdot a}{2} \]
\[ \mathrm{M_B}= \frac{q \cdot a}{2} \cdot (L- \frac 23 \cdot a) \]
Diagrama de cargas y reacciones caso 24

E. CORTANTES

\[ \mathrm{V_{AC}}= - \frac{q \cdot x^2}{2 \cdot a} \]
\[ \mathrm{V_{CB}}= -\frac{q \cdot a}{2} \]
Diagrama de Cortantes caso 24

M. FLECTORES

\[ \mathrm{M_{AC}}= - \frac{q \cdot x^3}{6 \cdot a} \]
\[ \mathrm{M_{CB}}= - \frac{q \cdot a}{2} \cdot (x- \frac 23 \cdot a) \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot a}{6} \cdot (3 \cdot L-2 \cdot a)| \hspace{2em} para \hspace{1em} x=L \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot a}{6} \cdot (3 \cdot L-2 \cdot a)| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 24

EC. ELÁSTICA

\[ \mathrm{Y_{CB}}=\frac {q \cdot a}{12 \cdot E \cdot I} \cdot ((x- \frac 23 \cdot a)^3-3 \cdot (L- \frac 23 \cdot a)^2 \cdot x+ ... \] \[ ... +2 \cdot (L- \frac 23 \cdot a)^2 \cdot (L+ \frac a3)) \]
\[ \mathrm{Y_{CB}}=\frac {q \cdot a}{12 \cdot E \cdot I} \cdot ((x- \frac 23 \cdot a)^3-3 \cdot (L- \frac 23 \cdot a)^2 \cdot x+ ... \] \[ ... +2 \cdot (L- \frac 23 \cdot a)^2 \cdot (L+ \frac a3)) \]
\[ \mathrm{Y_{AC}}=\frac {q}{E \cdot I} \cdot ( \frac {x^5}{120 \cdot a}- \frac{a^3}{72} \cdot x- \frac a4 \cdot (L- \frac 23 \cdot a)^2 \cdot x+ ... \] \[ ... + \frac{7 \cdot a^4}{810}+ \frac a6 \cdot (L- \frac 23 \cdot a)^2 \cdot (L+ \frac a3)) \]
\[ \mathrm{Y_{AC}}=\frac {q}{E \cdot I} \cdot ( \frac {x^5}{120 \cdot a}- \frac{a^3}{72} \cdot x- \frac a4 \cdot (L- \frac 23 \cdot a)^2 \cdot x+ ... \] \[ ... + \frac{7 \cdot a^4}{810}+ \frac a6 \cdot (L- \frac 23 \cdot a)^2 \cdot (L+ \frac a3)) \]

FLECHA

\[ \mathrm{Y_A}=\frac {q \cdot a}{30 \cdot E \cdot I} \cdot (a^3-15 \cdot a \cdot L^2+5 \cdot L^3) \]
Flecha caso 24

ÁNGULOS DE GIRO

\[ \mathrm{\theta_C}=\frac {q \cdot a}{36 \cdot E \cdot I} \cdot (a^2-(3 \cdot L-2 \cdot a)^2) \]
\[ \mathrm{\theta_A}=-\frac {q \cdot a}{72 \cdot E \cdot I} \cdot (a^2+2 \cdot (3 \cdot L-2 \cdot a)^2) \]


CASO 25

Diagrama forma y cargas caso 25

Definición

Viga en voladizo con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac{q \cdot L}{2} \]
\[ \mathrm{M_B}= \frac{q \cdot L^2}{6} \]
Diagrama de cargas y reacciones caso 25

E. CORTANTES

\[ \mathrm{V_x}= - \frac{q \cdot x^2}{2 \cdot L} \]
Diagrama de Cortantes caso 25

M. FLECTORES

\[ \mathrm{M_x}= - \frac{q \cdot x^3}{6 \cdot L} \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot L^2}{6}| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 25

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {q \cdot (L-x)^2}{24 \cdot E \cdot I} \cdot (2 \cdot L \cdot x+(L-x)^2- \frac{(L-x)^3}{5 \cdot L}) \]
\[ \mathrm{Y_x}=\frac {q \cdot (L-x)^2}{24 \cdot E \cdot I} \cdot (2 \cdot L \cdot x+(L-x)^2- \frac{(L-x)^3}{5 \cdot L}) \]

FLECHA

\[ \mathrm{Y_A}=\frac {q \cdot L^4}{30 \cdot E \cdot I} \]
Flecha caso 25

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\frac {q \cdot L^3}{24 \cdot E \cdot I} \]


CASO 26

Diagrama forma y cargas caso 26

Definición

Viga en voladizo con una carga no uniformemente repartida que comienza en el empotramiento según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac{q \cdot b}{2} \]
\[ \mathrm{M_B}= \frac{q \cdot b^2}{3} \]
Diagrama de cargas y reacciones caso 26

E. CORTANTES

\[ \mathrm{V_{AC}}= 0 \]
\[ \mathrm{V_{CB}}= -q \cdot \frac{b+L-x}{2 \cdot b} \cdot (x-a) \]
Diagrama de Cortantes caso 26

M. FLECTORES

\[ \mathrm{M_x}= - \frac{q \cdot (x-a)^2}{6 \cdot b} \cdot (2 \cdot b+L-x) \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot b^2}{3}| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 26

EC. ELÁSTICA

\[ \mathrm{Y_{CB}}=\frac {q}{120 \cdot E \cdot I \cdot b} \cdot (-(x-a)^5+5 \cdot b \cdot (x-a)^4-15 \cdot b^4 \cdot x-4 \cdot b^5 + 15 \cdot b^4 \cdot L) \]
\[ \mathrm{Y_{CB}}=\frac {q}{120 \cdot E \cdot I \cdot b} \cdot (-(x-a)^5+5 \cdot b \cdot (x-a)^4+ ... \] \[ ... -15 \cdot b^4 \cdot x-4 \cdot b^5 + 15 \cdot b^4 \cdot L) \]
\[ \mathrm{Y_{AC}}=\frac {q \cdot b^3}{120 \cdot E \cdot I} \cdot (-15 \cdot x-4 \cdot b+15 \cdot L) \]
\[ \mathrm{Y_{AC}}=\frac {q \cdot b^3}{120 \cdot E \cdot I} \cdot (-15 \cdot x-4 \cdot b+15 \cdot L) \]
\[ \mathrm{Y_C}=\frac {11 \cdot q \cdot b^4}{120 \cdot E \cdot I} \]

FLECHA

\[ \mathrm{Y_A}=\frac {q \cdot b^3}{120 \cdot E \cdot I} \cdot (-4 \cdot b+15 \cdot L) \]
Flecha caso 26

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\mathrm{\theta_C}=-\frac {q \cdot b^3}{8 \cdot E \cdot I} \]


CASO 27

Diagrama forma y cargas caso 27

Definición

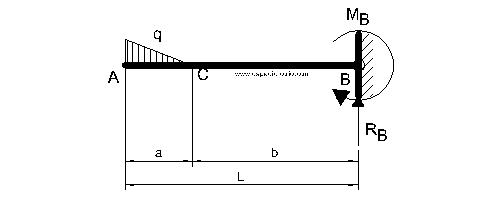
Viga en voladizo con una carga no uniformemente repartida que comienza en el extremo según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac{q \cdot a}{2} \]
\[ \mathrm{M_B}= \frac{q \cdot a}{2} \cdot (L- \frac a3) \]
Diagrama de cargas y reacciones caso 27

E. CORTANTES

\[ \mathrm{V_{AC}}= - \frac{q \cdot x}{2 \cdot a} \cdot (2 \cdot a-x) \]
\[ \mathrm{V_{CB}}= - \frac{q \cdot a}{2} \]
Diagrama de Cortantes caso 27

M. FLECTORES

\[ \mathrm{M_{AC}}= - \frac{q \cdot x^2}{6 \cdot a} \cdot (3 \cdot a-x) \]
\[ \mathrm{M_{CB}}= - \frac{q \cdot a}{2} \cdot (x- \frac 13 \cdot a) \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot a}{6} \cdot (3 \cdot L-a)| \hspace{2em} para \hspace{1em} x=L \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot a}{6} \cdot (3 \cdot L-a)| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 27

EC. ELÁSTICA

\[ \mathrm{Y_{CB}}=\frac {q \cdot a}{324 \cdot E \cdot I} \cdot ((3 \cdot x-a)^3-9 \cdot (3 \cdot L-a)^2 \cdot x+ ... \] \[ ... +(3 \cdot L-a)^2 \cdot (6 \cdot L+a)) \]
\[ \mathrm{Y_{CB}}=\frac {q \cdot a}{324 \cdot E \cdot I} \cdot ((3 \cdot x-a)^3-9 \cdot (3 \cdot L-a)^2 \cdot x+ ... \] \[ ... +(3 \cdot L-a)^2 \cdot (6 \cdot L+a)) \]
\[ \mathrm{Y_{AC}}=\frac {q}{120 \cdot E \cdot I} \cdot (- \frac {x^5}{a}+5 \cdot x^4-5 \cdot (5 \cdot a^3+4 \cdot a^2 \cdot L-6 \cdot a \cdot L^2) \cdot x+ ... \] \[ ... +21 \cdot a^4+40 \cdot a^3 \cdot L-70 \cdot a^2 \cdot L^2+20 \cdot a \cdot L^3) \]
\[ \mathrm{Y_{AC}}=\frac {q}{120 \cdot E \cdot I} \cdot ... \] \[ ... \cdot (- \frac {x^5}{a}+5 \cdot x^4-5 \cdot (5 \cdot a^3+4 \cdot a^2 \cdot L-6 \cdot a \cdot L^2) \cdot x+ ... \] \[ ... +21 \cdot a^4+40 \cdot a^3 \cdot L-70 \cdot a^2 \cdot L^2+20 \cdot a \cdot L^3) \]

FLECHA

\[ \mathrm{Y_A}=\frac {q \cdot a}{120 \cdot E \cdot I} \cdot (21 \cdot a^3+40 \cdot a^2 \cdot L-70 \cdot a \cdot L^2+20 \cdot L^3) \]
\[ \mathrm{Y_A}=\frac {q \cdot a}{120 \cdot E \cdot I} \cdot (21 \cdot a^3+40 \cdot a^2 \cdot L-70 \cdot a \cdot L^2+20 \cdot L^3) \]
Flecha caso 27

ÁNGULOS DE GIRO

\[ \mathrm{\theta_C}=-\frac {q \cdot a}{36 \cdot E \cdot I} \cdot (4 \cdot a^2-(3 \cdot L-a)^2) \]
\[ \mathrm{\theta_A}=-\frac {q \cdot a \cdot L}{24 \cdot E \cdot I} \cdot (5 \cdot a^3-4 \cdot a^2 \cdot L-6 \cdot a \cdot L^2) \]
\[ \mathrm{\theta_A}=-\frac {q \cdot a \cdot L}{24 \cdot E \cdot I} \cdot (5 \cdot a^3-4 \cdot a^2 \cdot L-6 \cdot a \cdot L^2) \]


CASO 28

Diagrama forma y cargas caso 28

Definición

Viga en voladizo con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac{q \cdot L}{2} \]
\[ \mathrm{M_B}= \frac{q \cdot L^2}{3} \]
Diagrama de cargas y reacciones caso 28

E. CORTANTES

\[ \mathrm{V_x}= - \frac{q \cdot x}{2 \cdot L} \cdot (2 \cdot L-x) \]
Diagrama de Cortantes caso 28

M. FLECTORES

\[ \mathrm{M_x}= - \frac{q \cdot x^2}{6 \cdot L} \cdot (3 \cdot L-x) \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot L^2}{3}| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 28

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {q}{120 \cdot E \cdot I \cdot L} \cdot (11 \cdot L^5-15 \cdot L^4 \cdot x+x^4 \cdot (5 \cdot L-x)) \]
\[ \mathrm{Y_x}=\frac {q}{120 \cdot E \cdot I \cdot L} \cdot (11 \cdot L^5-15 \cdot L^4 \cdot x+x^4 \cdot (5 \cdot L-x)) \]

FLECHA

\[ \mathrm{Y_A}=\frac {11 \cdot q \cdot L^4}{120 \cdot E \cdot I} \]
Flecha caso 28

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\frac {q \cdot L^3}{8 \cdot E \cdot I} \]


CASO 29

Diagrama forma y cargas caso 29

Definición

Viga en voladizo con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac{q \cdot L}{2} \]
\[ \mathrm{M_B}= \frac{q \cdot L \cdot (b+L)}{6} \]
Diagrama de cargas y reacciones caso 29

E. CORTANTES

\[ \mathrm{V_{AC}}= - \frac{q \cdot x^2}{2 \cdot a} \]
\[ \mathrm{V_{CB}}= - \frac{q \cdot a}{2}- \frac{q \cdot (x-a)}{2 \cdot b} \cdot (b+L-x) \]
Diagrama de Cortantes caso 29

M. FLECTORES

\[ \mathrm{M_{AC}}= - \frac{q \cdot x^3}{6 \cdot a} \]
\[ \mathrm{M_{CB}}= \frac{q \cdot 6 \cdot b}{2} \cdot (2 \cdot b \cdot a^2-3 \cdot b \cdot a \cdot x+(x-L-2 \cdot b)\cdot (x-a)^2) \]
\[ \mathrm{M_{CB}}= \frac{q \cdot 6 \cdot b}{2} \cdot (2 \cdot b \cdot a^2-3 \cdot b \cdot a \cdot x+ ... \] \[ ... +(x-L-2 \cdot b)\cdot (x-a)^2) \]
\[ \mathrm{M_{máx}}= |-\frac{q \cdot L \cdot (b+L)}{6}| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 29

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {q}{120 \cdot E \cdot I \cdot a} \cdot (x^2-5 \cdot a \cdot L) \cdot x +4 \cdot a^5+20 \cdot a^4 \cdot b+ ... \] \[ ... +a \cdot b^2 \cdot (29 \cdot a^2+13 \cdot a \cdot b+11 \cdot L^2)) \]
\[ \mathrm{Y_{AC}}=\frac {q}{120 \cdot E \cdot I \cdot a} \cdot ... \] \[ ... \cdot (x^2-5 \cdot a \cdot L) \cdot x +4 \cdot a^5+20 \cdot a^4 \cdot b+ ... \] \[ ... +a \cdot b^2 \cdot (29 \cdot a^2+13 \cdot a \cdot b+11 \cdot L^2)) \]
\[ \mathrm{Y_{CB}}=\frac {q}{120 \cdot E \cdot I \cdot b} \cdot (-x^5+5 \cdot L \cdot x^4-10 \cdot a \cdot L \cdot x^3+ ... \] \[ ... +10 \cdot a^2 \cdot L \cdot x^2-5 \cdot L^2 \cdot (a^2+3 \cdot b^2) \cdot x+L^3 \cdot (a^2+11 \cdot b^2+ 2 \cdot a \cdot b)) \]
\[ \mathrm{Y_{CB}}=\frac {q}{120 \cdot E \cdot I \cdot b} \cdot ... \] \[ ... \cdot (-x^5+5 \cdot L \cdot x^4-10 \cdot a \cdot L \cdot x^3+ ... \] \[ ... +10 \cdot a^2 \cdot L \cdot x^2-5 \cdot L^2 \cdot (a^2+3 \cdot b^2) \cdot x+ ... \] \[ ... +L^3 \cdot (a^2+11 \cdot b^2+ 2 \cdot a \cdot b)) \]

FLECHA

\[ \mathrm{Y_A}=\frac {q}{120 \cdot E \cdot I} \cdot (b^2 \cdot (29 \cdot a^2+13 \cdot a \cdot b+11 \cdot L^2)+4 \cdot a^4+20 \cdot a^3 \cdot b) \]
\[ \mathrm{Y_A}=\frac {q}{120 \cdot E \cdot I} \cdot ... \] \[ ... \cdot (b^2 \cdot (29 \cdot a^2+13 \cdot a \cdot b+11 \cdot L^2)+4 \cdot a^4+20 \cdot a^3 \cdot b) \]
Flecha caso 29

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\frac {q \cdot L}{24 \cdot E \cdot I} \cdot (a^2+3 \cdot b \cdot L) \]
\[ \mathrm{\theta_C}=-\frac {q \cdot b}{24 \cdot E \cdot I} \cdot (a^2+3 \cdot L^2) \]


CASO 30

Diagrama forma y cargas caso 30

Definición

Viga en voladizo con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_B}= \frac L2 \cdot (\mathrm{q_1}+\mathrm{q_2}) \]
\[ \mathrm{M_B}= \frac{L^2}{6} \cdot (\mathrm{q_2}+2 \cdot \mathrm{q_1}) \]
Diagrama de cargas y reacciones caso 30

E. CORTANTES

\[ \mathrm{V_x}= \frac{(\mathrm{q_1}-\mathrm{q_2})}{2 \cdot L} \cdot x^2- \mathrm{q_1} \cdot x \]
Diagrama de Cortantes caso 30

M. FLECTORES

\[ \mathrm{M_x}= \frac{((\mathrm{q_1}-\mathrm{q_2}) \cdot x-3 \cdot L \cdot \mathrm{q_1})}{6 \cdot L} \cdot x^2 \]
\[ \mathrm{M_{máx}}= |-\frac{L^2}{6} \cdot (\mathrm{q_2}+2 \cdot \mathrm{q_1})| \hspace{2em} para \hspace{1em} x=L \]
\[ \mathrm{M_{máx}}= |-\frac{L^2}{6} \cdot (\mathrm{q_2}+2 \cdot \mathrm{q_1})| \hspace{2em} para \hspace{1em} x=L \]
Diagrama de momentos caso 30

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {(L-x)^2}{24 \cdot E \cdot I} \cdot (- \frac {(L-x)^3}{5 \cdot L} \cdot (\mathrm{q_2}-\mathrm{q_1})+ ... \] \[ ... +(L-x)^2 \cdot \mathrm{q_2}-2 \cdot L \cdot(L-x) \cdot (\mathrm{q_2}+\mathrm{q_1})+ 2 \cdot L^2 \cdot (\mathrm{q_2}+2 \cdot \mathrm{q_1})) \]
\[ \mathrm{Y_x}=\frac {(L-x)^2}{24 \cdot E \cdot I} \cdot (- \frac {(L-x)^3}{5 \cdot L} \cdot (\mathrm{q_2}-\mathrm{q_1})+ ... \] \[ ... +(L-x)^2 \cdot \mathrm{q_2}-2 \cdot L \cdot(L-x) \cdot (\mathrm{q_2}+\mathrm{q_1})+ ... \] \[ ... + 2 \cdot L^2 \cdot (\mathrm{q_2}+2 \cdot \mathrm{q_1})) \]

FLECHA

\[ \mathrm{Y_A}=\frac {L^4 \cdot (4 \cdot \mathrm{q_2}+11 \cdot \mathrm{q_1})}{120 \cdot E \cdot I} \]
Flecha caso 30

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\frac {L^3 \cdot (3 \cdot \mathrm{q_1}+\mathrm{q_2})}{24 \cdot E \cdot I} \]


CASO 31

Diagrama forma y cargas caso 31

Definición

Viga en voladizo con un momento aislado según esquema.

REACCIONES

\[ \mathrm{M_B}= M \]
Diagrama de cargas y reacciones caso 31

E. CORTANTES

\[ \mathrm{V_x}= 0 \]
Diagrama de Cortantes caso 31

M. FLECTORES

\[ \mathrm{M_{AC}}= 0 \]
\[ \mathrm{M_{CB}}= -M \]
\[ \mathrm{M_{máx}}= |-M| \]
Diagrama de momentos caso 31

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {M \cdot b}{2 \cdot E \cdot I} \cdot (2 \cdot L-2 \cdot x -b) \]
\[ \mathrm{Y_{CB}}=\frac {M}{2 \cdot E \cdot I} \cdot (L-x)^2 \]
\[ \mathrm{Y_C}=\frac {M \cdot b^2}{2 \cdot E \cdot I} \]

FLECHA

\[ \mathrm{Y_A}=\frac {M}{2 \cdot E \cdot I} \cdot b \cdot (2 \cdot L-b) \]
Flecha caso 31

ÁNGULOS DE GIRO

\[ \mathrm{\theta_C}=\mathrm{\theta_A}=-\frac {M \cdot b}{E \cdot I} \]


CASO 32

Diagrama forma y cargas caso 32

Definición

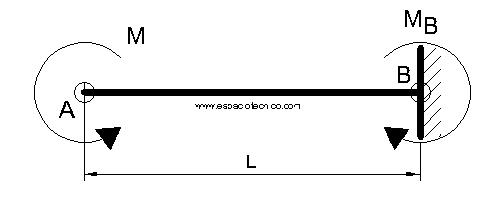
Viga en voladizo con un momento aislado en el extremo según esquema.

REACCIONES

\[ \mathrm{M_B}= M \]
Diagrama de cargas y reacciones caso 32

E. CORTANTES

\[ \mathrm{V_x}= 0 \]
Diagrama de Cortantes caso 32

M. FLECTORES

\[ \mathrm{M_x}= -M \]
\[ \mathrm{M_{máx}}= |-M| \]
Diagrama de momentos caso 32

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {M}{2 \cdot E \cdot I} \cdot (x^2-2 \cdot L \cdot x+L^2) \]

FLECHA

\[ \mathrm{Y_A}=\frac {M \cdot L^2}{2 \cdot E \cdot I} \]
Flecha caso 32

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=-\frac {M \cdot L}{E \cdot I} \]