Solicitamos su permiso para obtener datos estadísticos de su navegación en esta web, en cumplimiento del Real Decreto-ley 13/2012. Si continúa navegando consideramos que acepta el uso de cookies. OK | Más información
Compartir en WhatsApp, sólo para móviles.

VIGAS APOYADAS-EMPOTRADAS

RESUMEN DE CASOS

Pulsa en el diagrama para ir al caso elegido:

CASO 33

Diagrama forma y cargas caso 33

Definición

Viga apoyada-emportrada con una carga puntual intermedia.

REACCIONES

\[ \mathrm{R_A}=\frac{P \cdot b^2}{2 \cdot L^3} \cdot (3 \cdot L-b) \]
\[ \mathrm{R_B}=\frac{P \cdot a}{2 \cdot L^3} \cdot (3 \cdot L^2-a^2) \]
\[ \mathrm{M_B}=\frac{P \cdot a}{2 \cdot L^2} \cdot (L^2-a^2 \]
Diagrama de cargas y reacciones caso 33

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{P \cdot b^2}{2 \cdot L^3} \cdot (3 \cdot L-b) \]
\[ \mathrm{V_{CB}}=-\frac{P \cdot a}{2 \cdot L^3} \cdot (3 \cdot L^2-a^2) \]
Diagrama de Cortantes caso 33

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{P \cdot x}{2 \cdot L^3} \cdot b^2 \cdot (3 \cdot a+2 \cdot b) \]
\[ \mathrm{M_{CB}}=\frac{P \cdot a}{2 \cdot L^3} \cdot (2 \cdot L^3-3 \cdot L^2 \cdot x+a^2 \cdot x) \]
\[ \mathrm{M_C}=\frac{P \cdot a}{2 \cdot L^3} \cdot b^2 \cdot (3 \cdot a+2 \cdot b) \]
\[ M=0 \hspace{2em} para \hspace{1em} x=\frac{2 \cdot L^3}{3 \cdot L^2-a^2} \]
\[ \mathrm{M_{máx}}=| \mathrm{M_B} | \hspace{2em} para \hspace{1em} b < (2-\sqrt{2}) \cdot L \]
\[ \mathrm{M_{máx}}=| \mathrm{M_C} | \hspace{2em} para \hspace{1em} b > (2-\sqrt{2}) \cdot L \]
Diagrama de momentos caso 33

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{P \cdot b^2 \cdot x}{12 \cdot E \cdot I \cdot L^3} \cdot (3 \cdot a \cdot L^2-x^2 \cdot (2 \cdot L+a)) \]
\[ \mathrm{Y_{AC}}=\frac{P \cdot b^2 \cdot x}{12 \cdot E \cdot I \cdot L^3} \cdot ... \] \[ ... \cdot (3 \cdot a \cdot L^2-x^2 \cdot (2 \cdot L+a)) \]
\[ \mathrm{Y_{CB}}=\frac{P \cdot a \cdot (L-x)^2}{12 \cdot E \cdot I \cdot L^3} \cdot (3 \cdot L \cdot (L^2-a^2)-(3 \cdot L^2-a^2) \cdot (L+x)) \]
\[ \mathrm{Y_{CB}}=\frac{P \cdot a \cdot (L-x)^2}{12 \cdot E \cdot I \cdot L^3} \cdot ... \] \[ ... \cdot (3 \cdot L \cdot (L^2-a^2)-(3 \cdot L^2-a^2) \cdot (L+x)) \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{P \cdot b^2 \cdot a}{6 \cdot E \cdot I} \cdot \sqrt{\frac{a}{2 \cdot L+a}} \hspace{2em} para \hspace{1em} x=L \cdot \sqrt{\frac{a}{2 \cdot L+a}} \]
\[ \mathrm{Y_{máx}}=\frac{P \cdot b^2 \cdot a}{6 \cdot E \cdot I} \cdot \sqrt{\frac{a}{2 \cdot L+a}} \hspace{2em} para ... \] \[ ... para \hspace{1em} x=L \cdot \sqrt{\frac{a}{2 \cdot L+a}} \]
Flecha caso 33

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac{P \cdot a \cdot (L-a)^2}{4 \cdot E \cdot I \cdot L} \]
\[ \mathrm{\theta_C}=\frac{P \cdot a \cdot (L-a)^2}{4 \cdot E \cdot I \cdot L^3} \cdot (L^2-2 \cdot a \cdot L-a^2) \]


CASO 34

Diagrama forma y cargas caso 34

Definición

Viga apoyada-emportrada con una carga puntual centrada.

REACCIONES

\[ \mathrm{R_A}=\frac{5}{16} \cdot P \]
\[ \mathrm{R_B}=\frac{11}{16} \cdot P \]
\[ \mathrm{M_B}=\frac{3}{16} \cdot P \cdot L \]
Diagrama de cargas y reacciones caso 34

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{5}{16} \cdot P \]
\[ \mathrm{V_{CB}}=-\frac{11}{16} \cdot P \]
Diagrama de Cortantes caso 34

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{5}{16} \cdot P \cdot x \]
\[ \mathrm{M_{CB}}=-\frac{11}{16} \cdot P \cdot x+\frac 12 \cdot P \cdot L \]
\[ \mathrm{M_C}=\frac{5}{32} \cdot P \cdot L \]
\[ M=0 \hspace{2em} para \hspace{1em} x=\frac{8}{11} \cdot L=0,727 \cdot L \]
\[ \mathrm{M_{máx}}=|\mathrm{M_B} | \]
Diagrama de momentos caso 34

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac{P \cdot x}{96 \cdot E \cdot I} \cdot (3 \cdot L^2-5 \cdot x^2) \]
\[ \mathrm{Y_C}=\frac{7 \cdot P \cdot L^3}{768 \cdot E \cdot I} \]
\[ \mathrm{Y_{CB}}=\frac{P}{96 \cdot E \cdot I} \cdot (11 \cdot x-2 \cdot L) \cdot (L-x)^2 \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac{P \cdot L^3}{ E \cdot I \cdot 48 \cdot \sqrt{5}} \hspace{2em} para \hspace{1em} x=\frac{L}{\sqrt{5}} \]
Flecha caso 34

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac{P \cdot L^2}{32 \cdot E \cdot I} \]
\[ \mathrm{\theta_C}=-\frac{P \cdot L^2}{128 \cdot E \cdot I} \]


CASO 35

Diagrama forma y cargas caso 35

Definición

Viga apoyada-emportrada con dos cargas puntuales intermedias equidistantes a los extremos.

REACCIONES

\[ \mathrm{R_A}=\frac{P}{2 \cdot L^2} \cdot (2 \cdot L^2+3 \cdot a^2-3 \cdot a \cdot L) \]
\[ \mathrm{R_B}=\frac{P}{2 \cdot L^2} \cdot (2 \cdot L^2+3 \cdot a \cdot L-3 \cdot a^2) \]
\[ \mathrm{M_B}=\frac{3 \cdot P \cdot a}{2 \cdot L} \cdot (L-a) \]
Diagrama de cargas y reacciones caso 35

E. CORTANTES

\[ \mathrm{V_{AC}}=\frac{P}{2 \cdot L^2} \cdot (2 \cdot L^2+3 \cdot a^2-3 \cdot a \cdot L) \]
\[ \mathrm{V_{CD}}=\frac{3 \cdot P \cdot a}{2 \cdot L^2} \cdot (a-L) \]
\[ \mathrm{V_{DB}}=\frac{P}{2 \cdot L^2} \cdot (3 \cdot a^2-3 \cdot a \cdot L-2 \cdot L^2) \]
Diagrama de Cortantes caso 35

M. FLECTORES

\[ \mathrm{M_{AC}}=\frac{P}{2 \cdot L^2} \cdot (2 \cdot L^2+3 \cdot a^2-3 \cdot a \cdot L) \cdot x \]
\[ \mathrm{M_{CD}}=\frac{3 \cdot P \cdot a}{2 \cdot L^2} \cdot (a-L) \cdot x+P \cdot a \]
\[ \mathrm{M_{DB}}=\frac{P}{2 \cdot L^2} \cdot (3 \cdot a^2-3 \cdot a \cdot L-2 \cdot L^2) \cdot x+P \cdot L \]
\[ M=0 \hspace{2em} para \hspace{1em} x=\frac{2 \cdot L^3}{2 \cdot L^2+3 \cdot a \cdot L-3 \cdot a^2} \]
\[ \mathrm{M_{máx}}=|\mathrm{M_B}| \]
Diagrama de momentos caso 35

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {P \cdot x}{12 \cdot E \cdot I \cdot L^2} \cdot ((3 \cdot a \cdot L-3 \cdot a^2-2 \cdot L^2) \cdot x^2+3 \cdot a \cdot L^3-3 \cdot a^2 \cdot L^2) \]
\[ \mathrm{Y_{AC}}=\frac {P \cdot x}{12 \cdot E \cdot I \cdot L^2} \cdot ((3 \cdot a \cdot L-3 \cdot a^2-2 \cdot L^2) \cdot x^2+ ... \] \[ ... +3 \cdot a \cdot L^3-3 \cdot a^2 \cdot L^2) \]
\[ \mathrm{Y_{CD}}=\frac {P \cdot a}{12 \cdot E \cdot I \cdot L^2} \cdot (3 \cdot (L-a) \cdot x^3-6 \cdot L^2 \cdot x^2+3 \cdot L^2 \cdot (L+a) \cdot x-2 \cdot L^2 \cdot a^2) \]
\[ \mathrm{Y_{CD}}=\frac {P \cdot a}{12 \cdot E \cdot I \cdot L^2} \cdot (3 \cdot (L-a) \cdot x^3-6 \cdot L^2 \cdot x^2+ ... \] \[ ... +3 \cdot L^2 \cdot (L+a) \cdot x-2 \cdot L^2 \cdot a^2) \]
\[ \mathrm{Y_{DB}}=\frac {P \cdot (L-x)^2}{12 \cdot E \cdot I \cdot L^2} \cdot ((3 \cdot a^2-3 \cdot a \cdot L-2 \cdot L^2) \cdot x+2 \cdot L \cdot (3 \cdot a^2-3 \cdot a \cdot L+L^2)) \]
\[ \mathrm{Y_{DB}}=\frac {P \cdot (L-x)^2}{12 \cdot E \cdot I \cdot L^2} \cdot ((3 \cdot a^2-3 \cdot a \cdot L-2 \cdot L^2) \cdot x+ ... \] \[ ... +2 \cdot L \cdot (3 \cdot a^2-3 \cdot a \cdot L+L^2)) \]

FLECHA

\[ \mathrm{Y_{máx}} \hspace{2em} para \hspace{1em} x=\frac{2 \cdot L-\sqrt{L^2+3 \cdot a^2}}{3 \cdot (L-a) \cdot L} \]
Flecha caso 35

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac{P \cdot a \cdot (L-a)}{4 \cdot E \cdot I} \]


CASO 36

Diagrama forma y cargas caso 36

Definición

Viga apoyada-emportrada con una carga uniformemente repartida aislada.

REACCIONES

\[ \mathrm{M_B}=\frac {q \cdot a \cdot c}{8 \cdot L^2} \cdot (4 \cdot b \cdot (L+a)-c^2) \]
\[ \mathrm{R_A}=\frac 1L \cdot (q \cdot b \cdot c-\mathrm{M_B}) \]
\[ \mathrm{R_B}=\frac 1L \cdot (q \cdot a \cdot c+\mathrm{M_B}) \]
Diagrama de cargas y reacciones caso 36

E. CORTANTES

\[ \mathrm{V_{AC}}=\mathrm{R_A} \]
\[ \mathrm{V_{CD}}=\mathrm{R_A}- \frac q2 \cdot (2 \cdot (x-a)+c) \]
\[ \mathrm{V_{DB}}=-\mathrm{R_B} \]
Diagrama de Cortantes caso 36

M. FLECTORES

\[ \mathrm{M_{AC}}=\mathrm{R_A} \cdot x \]
\[ \mathrm{M_{CD}}=\mathrm{R_A} \cdot x- \frac q8 \cdot (2 \cdot (x-a)+c)^2 \]
\[ \mathrm{M_{DB}}=\mathrm{R_B} \cdot (L-x)- \mathrm{M_B} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}=\frac {\mathrm{R_A}^2}{2 \cdot q}+\mathrm{R_A} \cdot (a- \frac c2) \hspace{2em} para \hspace{1em} \mathrm{x_0}=(a- \frac c2)+ \frac{\mathrm{R_A}}{q} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}=\frac {\mathrm{R_A}^2}{2 \cdot q}+\mathrm{R_A} \cdot (a- \frac c2) \hspace{2em} para ... \] \[ ... para \hspace{1em} \mathrm{x_0}=(a- \frac c2)+ \frac{\mathrm{R_A}}{q} \]
\[ M=0 \hspace{2em} para \hspace{1em} x=(L- \frac{\mathrm{M_B}}{\mathrm{R_B}} \]
Diagrama de momentos caso 36

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {1}{48 \cdot E \cdot I \cdot L} \cdot (q \cdot c \cdot (L \cdot c^2-3 \cdot b \cdot c^2+12 \cdot a \cdot b^2)-8 \cdot \mathrm{R_A} \cdot L \cdot x^2) \cdot x \]
\[ \mathrm{Y_{AC}}=\frac {1}{48 \cdot E \cdot I \cdot L} \cdot ... \] \[ ... \cdot (q \cdot c \cdot (L \cdot c^2-3 \cdot b \cdot c^2+12 \cdot a \cdot b^2)-8 \cdot \mathrm{R_A} \cdot L \cdot x^2) \cdot x \]
\[ \mathrm{Y_{CD}}=\frac {1}{384 \cdot E \cdot I \cdot L} \cdot (8 \cdot q \cdot c \cdot (L \cdot c^2-3 \cdot b \cdot c^2+12 \cdot a \cdot b^2) \cdot x+ ... \] \[ ... -64 \cdot \mathrm{R_A} \cdot L \cdot x^3+q \cdot L \cdot (2 \cdot x -2 \cdot a + c)^4) \]
\[ \mathrm{Y_{CD}}=\frac {1}{384 \cdot E \cdot I \cdot L} \cdot ... \] \[ ... \cdot (8 \cdot q \cdot c \cdot (L \cdot c^2-3 \cdot b \cdot c^2+12 \cdot a \cdot b^2) \cdot x+ ... \] \[ ... -64 \cdot \mathrm{R_A} \cdot L \cdot x^3+q \cdot L \cdot (2 \cdot x -2 \cdot a + c)^4) \]
\[ \mathrm{Y_{DB}}=\frac {(L-x)^2}{6 \cdot E \cdot I} \cdot (3 \cdot \mathrm{M_B}- \mathrm{R_B} \cdot (L-x)) \]

FLECHA

Flecha caso 36

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac{q \cdot c}{48 \cdot E \cdot I \cdot L} \cdot (L \cdot c^2-3 \cdot b \cdot c^2+12 \cdot a \cdot b^2) \]


CASO 37

Diagrama forma y cargas caso 37

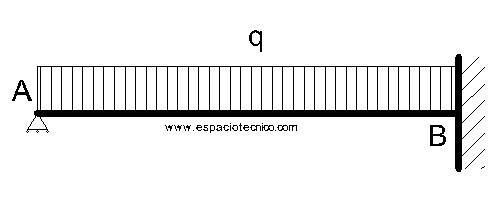
Definición

Viga apoyada-emportrada con una carga uniformemente repartida.

REACCIONES

\[ \mathrm{R_A}= \frac 38 \cdot q \cdot L \]
\[ \mathrm{R_B}= \frac 58 \cdot q \cdot L \]
\[ \mathrm{M_B}= \frac 18 \cdot q \cdot L^2 \]
Diagrama de cargas y reacciones caso 37

E. CORTANTES

\[ \mathrm{V_x}= \frac q8 \cdot (3 \cdot L-8 \cdot x) \]
Diagrama de Cortantes caso 37

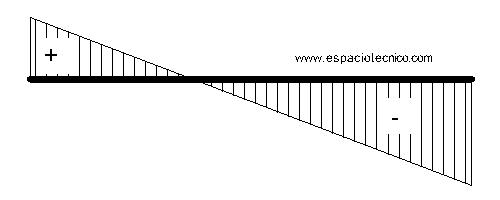
M. FLECTORES

\[ \mathrm{M_x}= \frac{q \cdot x}{8} \cdot (3 \cdot L-4 \cdot x) \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac{9}{128} \cdot q \cdot L^2 \hspace{2em} para \hspace{1em} x= \frac 38 \cdot L = 0,375 \cdot L \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac{9}{128} \cdot q \cdot L^2 \hspace{2em} para \hspace{1em} x= \frac 38 \cdot L = 0,375 \cdot L \]
\[ M=0 \hspace{2em} para \hspace{1em} x= \frac 34 \cdot L \]
\[ \mathrm{M_{máx}}= |\mathrm{M_B}| \]
Diagrama de momentos caso 37

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {q \cdot x}{48 \cdot E \cdot I} \cdot (L+2 \cdot x) \cdot (L-x)^2 \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac {q \cdot L^4}{185 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac{1+ \sqrt{33}}{16} \cdot L=0,422 \cdot L \]
\[ \mathrm{Y_{máx}}=\frac {q \cdot L^4}{185 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac{1+ \sqrt{33}}{16} \cdot L=0,422 \cdot L \]
Flecha caso 37

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac {q \cdot L^3}{48 \cdot E \cdot I} \]


CASO 38

Diagrama forma y cargas caso 38

Definición

Viga apoyada-emportrada con una carga no uniformemente repartida que comienza en el empotramiento según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot b^2}{6 \cdot L}- \frac{q \cdot b^2}{120 \cdot L^3} \cdot (20 \cdot L^2-15 \cdot b \cdot L+3 \cdot b^2) \]
\[ \mathrm{R_A}= \frac{q \cdot b^2}{6 \cdot L}- \frac{q \cdot b^2}{120 \cdot L^3} \cdot (20 \cdot L^2-15 \cdot b \cdot L+3 \cdot b^2) \]
\[ \mathrm{R_B}= \frac{q \cdot b}{6 \cdot L} \cdot (3 \cdot L)+ \frac{q \cdot b^2}{120 \cdot L^3} \cdot (20 \cdot L^2-15 \cdot b \cdot L+3 \cdot b^2) \]
\[ \mathrm{R_B}= \frac{q \cdot b}{6 \cdot L} \cdot (3 \cdot L)+ \frac{q \cdot b^2}{120 \cdot L^3} \cdot (20 \cdot L^2-15 \cdot b \cdot L+3 \cdot b^2) \]
\[ \mathrm{M_B}= \frac{q \cdot b^2}{120 \cdot L^2} \cdot (20 \cdot L^2-15 \cdot b \cdot L+3 \cdot b^2) \]
Diagrama de cargas y reacciones caso 38

E. CORTANTES

\[ \mathrm{V_{AC}}= \mathrm{R_{AC}} \]
\[ \mathrm{V_{CB}}= \mathrm{R_A}-\frac{q \cdot (x-a)^2}{2 \cdot b} \]
Diagrama de Cortantes caso 38

M. FLECTORES

\[ \mathrm{M_{AC}}= \mathrm{R_A} \cdot x \]
\[ \mathrm{M_{CB}}= \mathrm{R_A} \cdot x-\frac{q \cdot (x-a)^3}{6 \cdot b} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \mathrm{R_A} \cdot a+\frac{2 \cdot \mathrm{R_A}}{3} \cdot \sqrt{\frac{2 \cdot b}{q} \cdot \mathrm{R_A}} \hspace{2em} para \hspace{1em} \mathrm{x_0}=a+ \sqrt{\frac{2 \cdot b}{q} \cdot \mathrm{R_A}} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \mathrm{R_A} \cdot a+\frac{2 \cdot \mathrm{R_A}}{3} \cdot \sqrt{\frac{2 \cdot b}{q} \cdot \mathrm{R_A}} \hspace{2em} para ... \] \[ ... para \hspace{1em} \mathrm{x_0}=a+ \sqrt{\frac{2 \cdot b}{q} \cdot \mathrm{R_A}} \]
Diagrama de momentos caso 38

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot b} \cdot (-40 \cdot \mathrm{R_A} \cdot L \cdot x^2+q \cdot b^3 \cdot (5 \cdot L-3 \cdot b)) \]
\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot b} \cdot ... \] \[ ... \cdot (-40 \cdot \mathrm{R_A} \cdot L \cdot x^2+q \cdot b^3 \cdot (5 \cdot L-3 \cdot b)) \]
\[ \mathrm{Y_{CB}}=\frac {1}{240 \cdot E \cdot I \cdot b \cdot L} \cdot (2 \cdot q \cdot L \cdot(x-a)^5-40 \cdot \mathrm{R_A} \cdot b \cdot L \cdot x^3+ ... \] \[ ... +q \cdot b^4 \cdot (5 \cdot L-3 \cdot b) \cdot x) \]
\[ \mathrm{Y_{CB}}=\frac {1}{240 \cdot E \cdot I \cdot b \cdot L} \cdot ... \] \[ ... \cdot (2 \cdot q \cdot L \cdot(x-a)^5-40 \cdot \mathrm{R_A} \cdot b \cdot L \cdot x^3+ ... \] \[ ... +q \cdot b^4 \cdot (5 \cdot L-3 \cdot b) \cdot x) \]

FLECHA

Flecha caso 38

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac {q \cdot b^3}{240 \cdot E \cdot I \cdot L} \cdot (5 \cdot L-3 \cdot b) \]


CASO 39

Diagrama forma y cargas caso 39

Definición

Viga apoyada-emportrada con una carga no uniformemente repartida que comienza en el apoyo según esquema.

REACCIONES

\[ \mathrm{M_B}= \frac{q \cdot a^2}{30 \cdot L^2} \cdot (5 \cdot L^2-3 \cdot a^2) \]
\[ \mathrm{R_A}= \frac{q \cdot a}{6 \cdot L} \cdot (3 \cdot L-2 \cdot a)- \frac{\mathrm{M_B}}{L} \]
\[ \mathrm{R_B}= \frac{1}{3 \cdot L} \cdot (q \cdot a^2-3 \cdot \mathrm{M_B}) \]
Diagrama de cargas y reacciones caso 39

E. CORTANTES

\[ \mathrm{V_{AC}}= \mathrm{R_A}- \frac{q \cdot x^2}{2 \cdot a} \]
\[ \mathrm{V_{BC}}= -\mathrm{R_B} \]
Diagrama de Cortantes caso 39

M. FLECTORES

\[ \mathrm{M_AC}= \mathrm{R_A} \cdot x- \frac{q \cdot x^3}{6 \cdot a} \]
\[ \mathrm{M_CB}= \mathrm{R_B} \cdot (L-x)- \mathrm{M_B} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac 23 \cdot \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}^3} \hspace{2em} para \hspace{1em} \mathrm{x_0}= \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac 23 \cdot \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}^3} \hspace{2em} para \hspace{1em} \mathrm{x_0}= \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}} \]
\[ M=0 \hspace{2em} para \hspace{1em} x= \frac{q \cdot a^2}{3 \cdot \mathrm{R_B}} \]
Diagrama de momentos caso 39

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {x}{120 \cdot E \cdot I \cdot a \cdot L} \cdot (q \cdot L \cdot x^4-20 \cdot \mathrm{R_A} \cdot a \cdot L \cdot x^2 + ... \] \[ ... + q \cdot a^3 \cdot (10 \cdot L^2-15 \cdot a \cdot L+6 \cdot a^2)) \]
\[ \mathrm{Y_{AC}}=\frac {x}{120 \cdot E \cdot I \cdot a \cdot L} \cdot (q \cdot L \cdot x^4-20 \cdot \mathrm{R_A} \cdot a \cdot L \cdot x^2 + ... \] \[ ... + q \cdot a^3 \cdot (10 \cdot L^2-15 \cdot a \cdot L+6 \cdot a^2)) \]
\[ \mathrm{Y_{CB}}=\frac {(L-x)^2}{6 \cdot E \cdot I} \cdot (\mathrm{R_B} \cdot (x-L)+3 \cdot \mathrm{M_B}) \]

FLECHA

Flecha caso 39

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac {q \cdot a^2}{120 \cdot E \cdot I \cdot L} \cdot (10 \cdot L^2-15 \cdot a \cdot L+6 \cdot a^2) \]
\[ \mathrm{\theta_A}=\frac {q \cdot a^2}{120 \cdot E \cdot I \cdot L} \cdot (10 \cdot L^2-15 \cdot a \cdot L+6 \cdot a^2) \]


CASO 40

Diagrama forma y cargas caso 40

Definición

Viga apoyada-emportrada con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot L}{10} \]
\[ \mathrm{R_B}= \frac{4}{10} \cdot q \cdot b \]
\[ \mathrm{M_B}= \frac{q \cdot L^2}{15} \]
Diagrama de cargas y reacciones caso 40

E. CORTANTES

\[ \mathrm{V_x}= \frac{q}{10 \cdot L} \cdot (L^2-5 \cdot x^2) \]
Diagrama de Cortantes caso 40

M. FLECTORES

\[ \mathrm{M_x}= \frac{q \cdot x}{30 \cdot L} \cdot (3 \cdot L^2-5 \cdot x^2) \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac{q \cdot L^2}{15 \cdot \sqrt{5}} \hspace{2em} para \hspace{1em} \mathrm{x_0}= \frac{L}{\sqrt{5}}=0,477 \cdot L \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac{q \cdot L^2}{15 \cdot \sqrt{5}} \hspace{2em} para \hspace{1em} \mathrm{x_0}= \frac{L}{\sqrt{5}}=0,477 \cdot L \]
\[ \mathrm{M_{máx}}= |\mathrm{M_B}| \]
\[ M=0 \hspace{2em} para \hspace{1em} x= \frac{\sqrt{15}}{5} \cdot L=0,775 \cdot L \]
Diagrama de momentos caso 40

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {q \cdot x}{120 \cdot E \cdot I \cdot L} \cdot (L^2-x^2)^2 \]

FLECHA

\[ \mathrm{Y_{máx}}=\frac {2 \cdot q \cdot L^4}{375 \cdot \sqrt{5} \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac{L}{\sqrt{5}} \]
Flecha caso 40

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac {q \cdot L^2}{120 \cdot E \cdot I} \]


CASO 41

Diagrama forma y cargas caso 41

Definición

Viga apoyada-emportrada con una carga no uniformemente repartida que comienza en el empotramiento según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot b^2}{3 \cdot L}- \frac{q \cdot b^2}{120 \cdot L^3} \cdot (40 \cdot L^2-45 \cdot b \cdot L+12 \cdot b^2) \]
\[ \mathrm{R_A}= \frac{q \cdot b^2}{3 \cdot L}- \frac{q \cdot b^2}{120 \cdot L^3} \cdot (40 \cdot L^2-45 \cdot b \cdot L+12 \cdot b^2) \]
\[ \mathrm{R_B}= \frac{q \cdot b}{6 \cdot L} \cdot (3 \cdot L-2 \cdot b)- \frac{q \cdot b^2}{120 \cdot L^3} \cdot (40 \cdot L^2-45 \cdot b \cdot L+12 \cdot b^2) \]
\[ \mathrm{R_B}= \frac{q \cdot b}{6 \cdot L} \cdot (3 \cdot L-2 \cdot b)+ ... \] \[ ... - \frac{q \cdot b^2}{120 \cdot L^3} \cdot (40 \cdot L^2-45 \cdot b \cdot L+12 \cdot b^2) \]
\[ \mathrm{M_B}= \frac{q \cdot b^2}{120 \cdot L^2} \cdot (40 \cdot L^2-45 \cdot b \cdot L+12 \cdot b^2) \]
Diagrama de cargas y reacciones caso 41

E. CORTANTES

\[ \mathrm{V_{AC}}= \mathrm{R_A} \]
\[ \mathrm{V_{CB}}= \mathrm{R_A}- \frac{q}{2 \cdot b} \cdot (b+L-x) \cdot (x-a) \]
Diagrama de Cortantes caso 41

M. FLECTORES

\[ \mathrm{M_{AC}}= \mathrm{R_A} \cdot x \]
\[ \mathrm{M_{CB}}= \mathrm{R_A} \cdot x- \frac{q}{6 \cdot b} \cdot (2 \cdot b+L-x) \cdot (x-a)^2 \]
\[ \mathrm{M_{CB}}= \mathrm{R_A} \cdot x- \frac{q}{6 \cdot b} \cdot (2 \cdot b+L-x) \cdot (x-a)^2 \]
\[ \mathrm{M_{máx \hspace{1em} rel}} \hspace{1em} para \hspace{1em} \mathrm{x_0}=L- \sqrt{L^2-(a^2+2 \cdot b \cdot (a+ \frac{\mathrm{R_A}}{q}))} \]
\[ \mathrm{M_{máx \hspace{1em} rel}} \hspace{1em} para \hspace{1em} \mathrm{x_0}=L- \sqrt{L^2-(a^2+2 \cdot b \cdot (a+ \frac{\mathrm{R_A}}{q}))} \]
Diagrama de momentos caso 41

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot L} \cdot (-40 \cdot \mathrm{R_A} \cdot L \cdot x^2+3 \cdot q \cdot b^3 \cdot (5 \cdot L-4 \cdot b)) \]
\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot L} \cdot ... \] \[ ... \cdot (-40 \cdot \mathrm{R_A} \cdot L \cdot x^2+3 \cdot q \cdot b^3 \cdot (5 \cdot L-4 \cdot b)) \]
\[ \mathrm{Y_{CB}}=\frac {1}{240 \cdot E \cdot I \cdot b \cdot L} \cdot (-2 \cdot q \cdot L \cdot (x-a)^5+10 \cdot q \cdot b \cdot L \cdot (x-a)^4+ ... \] \[ ... -40\cdot \mathrm{R_A} \cdot b \cdot L \cdot x^3 +3 \cdot q \cdot b^4 \cdot (5 \cdot L-4 \cdot b) \cdot x) \]
\[ \mathrm{Y_{CB}}=\frac {1}{240 \cdot E \cdot I \cdot b \cdot L} \cdot ... \] \[ ... \cdot (-2 \cdot q \cdot L \cdot (x-a)^5+10 \cdot q \cdot b \cdot L \cdot (x-a)^4+ ... \] \[ ... -40\cdot \mathrm{R_A} \cdot b \cdot L \cdot x^3 +3 \cdot q \cdot b^4 \cdot (5 \cdot L-4 \cdot b) \cdot x) \]

FLECHA

Flecha caso 41

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac {q \cdot b^3}{80 \cdot E \cdot I \cdot L} \cdot (5 \cdot L-(4 \cdot b) \]


CASO 42

Diagrama forma y cargas caso 42

Definición

Viga apoyada-emportrada con una carga no uniformemente repartida que comienza en el apoyo según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac{q \cdot a}{6 \cdot L} \cdot (3 \cdot L-a)- \frac{\mathrm{M_B}}{L} \]
\[ \mathrm{R_B}= \frac{q \cdot a^2}{6 \cdot L}+ \frac{\mathrm{M_B}}{L} \]
\[ \mathrm{M_B}= \frac{q \cdot a^2}{120 \cdot L^2} \cdot (10 \cdot L^2-3 \cdot a^2) \]
Diagrama de cargas y reacciones caso 42

E. CORTANTES

\[ \mathrm{V_{AC}}= \mathrm{R_A}- \frac{q \cdot x}{2} \cdot (2 \cdot a-x) \]
\[ \mathrm{V_{CB}}= -\mathrm{R_B} \]
Diagrama de Cortantes caso 42

M. FLECTORES

\[ \mathrm{M_{AC}}= \mathrm{R_A} \cdot x- \frac{q \cdot x^2}{6 \cdot a} \cdot (3 \cdot a-x) \]
\[ \mathrm{M_{CB}}= \mathrm{R_B} \cdot (L-x)-\mathrm{M_B} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \hspace{2em} para \hspace{1em} \mathrm{x_0}=a- \sqrt{a^2- \frac 2q \cdot \mathrm{R_A}} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \hspace{2em} para \hspace{1em} \mathrm{x_0}=a- \sqrt{a^2- \frac 2q \cdot \mathrm{R_A}} \]
\[ M=0 \hspace{2em} para \hspace{1em} x=a- \frac{q \cdot a^2}{6 \cdot \mathrm{R_B}} \]
Diagrama de momentos caso 42

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot a \cdot L} \cdot (-2 \cdot q \cdot L \cdot x^4+10 \cdot q \cdot a \cdot L \cdot x^3-40 \cdot \mathrm{R_A} \cdot a \cdot L \cdot x^2+ ... \] \[ ... +q \cdot a^3 \cdot (10 \cdot L^2-10 \cdot a \cdot L+3 \cdot a^2)) \]
\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot a \cdot L} \cdot ... \] \[ ... \cdot (-2 \cdot q \cdot L \cdot x^4+10 \cdot q \cdot a \cdot L \cdot x^3-40 \cdot \mathrm{R_A} \cdot a \cdot L \cdot x^2+ ... \] \[ ... +q \cdot a^3 \cdot (10 \cdot L^2-10 \cdot a \cdot L+3 \cdot a^2)) \]
\[ \mathrm{Y_{CB}}=\frac {(L-x)^2}{6 \cdot E \cdot I} \cdot (\mathrm{R_B} \cdot (x-L)+3 \cdot \mathrm{M_B}) \]

FLECHA

Flecha caso 42

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac {q \cdot a^2}{240 \cdot E \cdot I \cdot L} \cdot (10 \cdot L^2-10 \cdot a \cdot L+3 \cdot a^2) \]
\[ \mathrm{\theta_A}= \frac {q \cdot a^2}{240 \cdot E \cdot I \cdot L} \cdot (10 \cdot L^2-10 \cdot a \cdot L+3 \cdot a^2) \]


CASO 43

Diagrama forma y cargas caso 43

Definición

Viga apoyada-empotrada con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac{11}{40} \cdot q \cdot L \]
\[ \mathrm{R_B}= \frac{9}{40} \cdot q \cdot L \]
\[ \mathrm{M_B}= \frac{7}{120} \cdot q \cdot L^2 \]
Diagrama de cargas y reacciones caso 43

E. CORTANTES

\[ \mathrm{V_x}= \frac{q}{40 \cdot L} \cdot (20 \cdot x^2-40 \cdot x \cdot L+11 \cdot L^2) \]
Diagrama de Cortantes caso 43

M. FLECTORES

\[ \mathrm{M_x}= \frac{q \cdot x}{120 \cdot L} \cdot (20 \cdot x^2-60 \cdot L \cdot x+33 \cdot L^2) \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac{q \cdot L^2}{600} \cdot (27 \cdot \sqrt{5}-35) \hspace{2em} para \hspace{1em} \mathrm{x_0}= \frac{L}{10} \cdot (10-3 \cdot \sqrt{5})=0,329 \cdot L \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac{q \cdot L^2}{600} \cdot (27 \cdot \sqrt{5}-35) \hspace{2em} para ... \] \[ ... para \hspace{1em} \mathrm{x_0}= \frac{L}{10} \cdot (10-3 \cdot \sqrt{5})=0,329 \cdot L \]
\[ \mathrm{M_{máx}}= |\mathrm{M_B}| \]
\[ M=0 \hspace{2em} para \hspace{1em} x= \frac{L}{10} \cdot (15-2 \cdot \sqrt{15})=0,725 \cdot L \]
\[ M=0 \hspace{2em} para \hspace{1em} x= \frac{L}{10} \cdot (15-2 \cdot \sqrt{15})=0,725 \cdot L \]
Diagrama de momentos caso 43

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {q \cdot x \cdot (L-x)^2}{240 \cdot E \cdot I \cdot L} \cdot (-2 \cdot x^2+6 \cdot L \cdot x+3 \cdot L^2) \]
\[ \mathrm{Y_x}=\frac {q \cdot x \cdot (L-x)^2}{240 \cdot E \cdot I \cdot L} \cdot (-2 \cdot x^2+6 \cdot L \cdot x+3 \cdot L^2) \]

FLECHA

\[ \mathrm{Y_{máx}}=0,003 \cdot \frac {q \cdot L^4}{E \cdot I} \hspace{2em} para \hspace{1em} x=0,598 \cdot L \]
\[ \mathrm{Y_{máx}}=0,003 \cdot \frac {q \cdot L^4}{E \cdot I} \hspace{2em} para \hspace{1em} x=0,598 \cdot L \]
Flecha caso 43

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac {q \cdot L^3}{80 \cdot E \cdot I} \]


CASO 44

Diagrama forma y cargas caso 44

Definición

Viga apoyada-empotrada con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac q6 \cdot (L+b)- \frac{\mathrm{M_B}}{L} \]
\[ \mathrm{R_B}= \frac q6 \cdot (L+a)+ \frac{\mathrm{M_B}}{L} \]
\[ \mathrm{M_B}= \frac{q \cdot (L+a)}{120 \cdot L} \cdot (7 \cdot L^2-3 \cdot a^2) \]
Diagrama de cargas y reacciones caso 44

E. CORTANTES

\[ \mathrm{V_{AC}}= \mathrm{R_A}- \frac{q \cdot x^2}{2 \cdot a} \]
\[ \mathrm{V_{CB}}= -\mathrm{R_B}+ \frac{q \cdot (L-x)^2}{2 \cdot b} \]
Diagrama de Cortantes caso 44

M. FLECTORES

\[ \mathrm{M_{AC}}= \mathrm{R_A} \cdot x- \frac{q \cdot x^3}{6 \cdot a} \]
\[ \mathrm{M_{CB}}= \mathrm{R_B} \cdot (L-x)- \frac{q \cdot (L-x)^3}{6 \cdot b}+\mathrm{M_B} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac 23 \cdot \mathrm{R_A} \cdot \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}} \hspace{2em} para \hspace{1em} \mathrm{x_0}= \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}} \]
\[ \mathrm{M_{máx \hspace{1em} rel}}= \frac 23 \cdot \mathrm{R_A} \cdot \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}} \hspace{2em} para ... \] \[ ... para \hspace{1em} \mathrm{x_0}= \sqrt{\frac{2 \cdot a}{q} \cdot \mathrm{R_A}} \]
Diagrama de momentos caso 44

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot a} \cdot (2 \cdot q \cdot x^4-40 \mathrm{R_A} \cdot a \cdot x^2+ ... \] \[ ... +q \cdot a \cdot (3 \cdot L^3+3 \cdot a \cdot L^2-7 \cdot a^2 \cdot L+3 \cdot a^3)) \]
\[ \mathrm{Y_{AC}}=\frac {x}{240 \cdot E \cdot I \cdot a} \cdot (2 \cdot q \cdot x^4-40 \mathrm{R_A} \cdot a \cdot x^2+ ... \] \[ ... +q \cdot a \cdot (3 \cdot L^3+3 \cdot a \cdot L^2-7 \cdot a^2 \cdot L+3 \cdot a^3)) \]
\[ \mathrm{Y_{CB}}=\frac {(L-x)^2}{120 \cdot E \cdot I \cdot b} \cdot (q \cdot (L-x)^3-20 \mathrm{R_B} \cdot b \cdot (L-x)+60 \cdot \mathrm{M_B} \cdot b) \]
\[ \mathrm{Y_{CB}}=\frac {(L-x)^2}{120 \cdot E \cdot I \cdot b} \cdot (q \cdot (L-x)^3 + ... \] \[ ... - 20 \mathrm{R_B} \cdot b \cdot (L-x)+60 \cdot \mathrm{M_B} \cdot b) \]

FLECHA

Flecha caso 44

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac {q}{80 \cdot E \cdot I} \cdot (L^3+a \cdot L^2- \frac 73 \cdot a^2 \cdot L+a^3) \]
\[ \mathrm{\theta_A}= \frac {q}{80 \cdot E \cdot I} \cdot (L^3+a \cdot L^2- \frac 73 \cdot a^2 \cdot L+a^3) \]


CASO 45

Diagrama forma y cargas caso 45

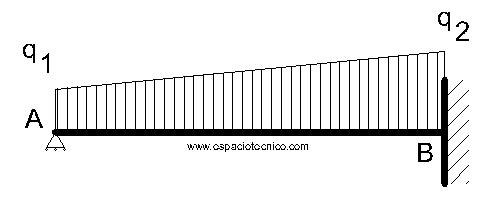
Definición

Viga apoyada-empotrada con una carga no uniformemente repartida según esquema.

REACCIONES

\[ \mathrm{R_A}= \frac L6 \cdot (2 \cdot \mathrm{q_1}+\mathrm{q_2})- \frac{ \mathrm{M_B}}{L} \]
\[ \mathrm{R_B}= \frac L6 \cdot (\mathrm{q_1}+2 \cdot \mathrm{q_2})+ \frac{ \mathrm{M_B}}{L} \]
\[ \mathrm{M_B}= \frac{L^2}{120} \cdot (7 \cdot \mathrm{q_1}+8 \cdot \mathrm{q_2}) \]
Diagrama de cargas y reacciones caso 45

E. CORTANTES

\[ \mathrm{V_x}= \mathrm{R_A}- \frac{(\mathrm{q_1} \cdot (2 \cdot L-x)+\mathrm{q_2} \cdot x)}{2 \cdot L} \cdot x \]
\[ \mathrm{V_B}= -\mathrm{R_B} \]
Diagrama de Cortantes caso 45

M. FLECTORES

\[ \mathrm{M_x}= \mathrm{R_A} \cdot x- \frac{(\mathrm{q_1} \cdot (3 \cdot L-x)+\mathrm{q_2} \cdot x)}{6 \cdot L} \]
Diagrama de momentos caso 45

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {x}{120 \cdot E \cdot I \cdot L} \cdot ((\mathrm{q_2}-\mathrm{q_1}) \cdot x^4+5 \cdot L \cdot \mathrm{q_1} \cdot x^3+ ... \] \[ ... -20 \cdot \mathrm{R_A} \cdot L \cdot x^2+5 \cdot L \cdot (12 \cdot \mathrm{R_A} \cdot L^2-(3 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L^3)) \]
\[ \mathrm{Y_x}=\frac {x}{120 \cdot E \cdot I \cdot L} \cdot ((\mathrm{q_2}-\mathrm{q_1}) \cdot x^4+5 \cdot L \cdot \mathrm{q_1} \cdot x^3+ ... \] \[ ... -20 \cdot \mathrm{R_A} \cdot L \cdot x^2+5 \cdot L \cdot (12 \cdot \mathrm{R_A} \cdot L^2-(3 \cdot \mathrm{q_1}+\mathrm{q_2}) \cdot L^3)) \]

FLECHA

Flecha caso 45

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}= \frac {L^3}{240 \cdot E \cdot I} \cdot (3 \cdot \mathrm{q_1}+2 \cdot \mathrm{q_2}) \]


CASO 46

Diagrama forma y cargas caso 46

Definición

Viga apoyada-empotrada con un momento aislado según esquema.

REACCIONES

\[ \mathrm{R_A}= \mathrm{R_B}= \frac{3 \cdot \mathrm{M_C}}{2 \cdot L^3} \cdot (L^2-a^2) \]
\[ \mathrm{M_B}= \frac{\mathrm{M_C}}{2 \cdot L^2} \cdot (L^2-3 \cdot a^2) \]
\[ NOTA: \hspace{1em} \mathrm{M_B} \hspace{1em} cambia \hspace{1em} de \hspace{1em} sentido \hspace{1em} cuando \hspace{1em} a < \frac{L}{\sqrt{3}}=0,577 \cdot L \]
\[ NOTA: \hspace{1em} \mathrm{M_B} \hspace{1em} cambia \hspace{1em} de \hspace{1em} sentido ... \] \[ ... cuando \hspace{1em} a < \frac{L}{\sqrt{3}}=0,577 \cdot L \]
Diagrama de cargas y reacciones caso 46

E. CORTANTES

\[ \mathrm{V_x}= \mathrm{R_A} \]
Diagrama de Cortantes caso 46

M. FLECTORES

\[ \mathrm{M_{AC}}= \frac{3 \cdot \mathrm{M_C}}{2 \cdot L^3} \cdot (L^2-a^2) \cdot x \]
\[ \mathrm{M_{CB}}= \frac{3 \cdot \mathrm{M_C}}{2 \cdot L^3} \cdot (L^2-a^2) \cdot x-\mathrm{M_C} \]
\[ \mathrm{M_{x=a}}^dcha= a \cdot \mathrm{R_A}-\mathrm{M_C} \]
\[ \mathrm{M_{x=a}}^izq= a \cdot \mathrm{R_A} \]
\[ \mathrm{M_{máx}}= |\mathrm{M_{x=a}}^dcha| \hspace{2em} para \hspace{1em} a < 0,395 \cdot L \hspace{1em} ó \hspace{1em} a > 0,742 \cdot L \]
\[ \mathrm{M_{máx}}= |\mathrm{M_{x=a}}^dcha| \hspace{2em} para ... \] \[ ... para \hspace{1em} a < 0,395 \cdot L \hspace{1em} ó \hspace{1em} a > 0,742 \cdot L \]
\[ \mathrm{M_{máx}}= |\mathrm{M_{x=a}}^izq| \hspace{2em} para \hspace{1em} 0,395 < a < 0,742 \cdot L \]
\[ \mathrm{M_{máx}}= |\mathrm{M_{x=a}}^izq| \hspace{2em} para \hspace{1em} 0,395 < a < 0,742 \cdot L \]
\[ Cuando \hspace{1em} a < \frac{L}{\sqrt{3}} \hspace{1em} M=0 \hspace{2em} para \hspace{1em} x= \frac{2 \cdot L^3}{L^2-a^2} \]
\[ Cuando \hspace{1em} a < \frac{L}{\sqrt{3}} \hspace{1em} M=0 \hspace{2em} para \hspace{1em} x= \frac{2 \cdot L^3}{L^2-a^2} \]
Diagrama de momentos caso 46

EC. ELÁSTICA

\[ \mathrm{Y_{AC}}=\frac {\mathrm{M_C} \cdot b \cdot x}{4 \cdot E \cdot I \cdot L^3} \cdot (4 \cdot L^3-(x^2-3 \cdot L^2)\cdot (a+L)) \]
\[ \mathrm{Y_{AC}}=\frac {\mathrm{M_C} \cdot b \cdot x}{4 \cdot E \cdot I \cdot L^3} \cdot (4 \cdot L^3-(x^2-3 \cdot L^2)\cdot (a+L)) \]
\[ \mathrm{Y_{CB}}=\frac {\mathrm{M_C}}{4 \cdot E \cdot I \cdot L^3} \cdot ((L-x)^2 \cdot (2 \cdot a^2 \cdot L-x \cdot (L^2-a^2)) \]
\[ \mathrm{Y_{CB}}=\frac {\mathrm{M_C}}{4 \cdot E \cdot I \cdot L^3} \cdot ((L-x)^2 \cdot (2 \cdot a^2 \cdot L-x \cdot (L^2-a^2)) \]

FLECHA

Flecha caso 46

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac {\mathrm{M_C}}{4 \cdot E \cdot I \cdot L} \cdot (L-a) \cdot (3 \cdot a-L) \]
\[ \mathrm{\theta_C}=\frac {\mathrm{M_C} \cdot b}{4 \cdot E \cdot I \cdot L^3} \cdot (3 \cdot b \cdot (L+a)^2-4 \cdot L^3) \]


CASO 47

Diagrama forma y cargas caso 47

Definición

Viga apoyada-empotrada con un momento aislado en el apoyo según esquema.

REACCIONES

\[ \mathrm{R_A}=\mathrm{R_B}= \frac{3 \cdot \mathrm{M_a}}{2 \cdot L} \]
\[ \mathrm{M_B}= \frac{\mathrm{M_a}}{2} \]
Diagrama de cargas y reacciones caso 47

E. CORTANTES

\[ \mathrm{V_x}= -\mathrm{R_B}= \frac{3 \cdot \mathrm{M_a}}{2 \cdot L} \]
Diagrama de Cortantes caso 47

M. FLECTORES

\[ \mathrm{M_x}= \mathrm{M_a}-\mathrm{R_B}= \frac{3 \cdot \mathrm{M_a}}{2 \cdot L} \cdot x \]
\[ \mathrm{M_{máx}}= \mathrm{M_a} \hspace{2em} para \hspace{1em} x=0 \]
Diagrama de momentos caso 47

EC. ELÁSTICA

\[ \mathrm{Y_x}=\frac {\mathrm{M_a} \cdot x}{4 \cdot E \cdot I \cdot L} \cdot (L-x)^2 \]

FLECHA

\[ \mathrm{Y_{máx}}= \frac {\mathrm{M_a} \cdot L^2}{27 \cdot E \cdot I} \hspace{2em} para \hspace{1em} x= \frac L3 \]
Flecha caso 47

ÁNGULOS DE GIRO

\[ \mathrm{\theta_A}=\frac {\mathrm{M_a} \cdot L}{4 \cdot E \cdot I} \]